Lý thuyết và bài tập về dấu tam thức bậc hai
Xem thêm về lý thuyết tam thức bậc hai, tam thức bậc 2
Định lí Viet thuận và đảo trong phương trình bậc hai -tam thức bậc hai
Tam thức bậc hai luôn âm khi nào? Khi a<0 và delta<0
Tam thức bậc hai luôn dương khi nào? khi a>0 và delta<0
Các bài tập về tam thức bậc 2 lớp 8
Các bài tập về tam thức bậc 2 lớp 10
A.Lý thuyết về dấu tam thức bậc hai
1. Tam thức bậc hai (một ẩn) là đa thức có dạng f(x) = ax2 + bx + c trong đó x là biến a, b, c là các số đã cho, với a ≠ 0.
Định lí. Cho tam thức bậc hai f(x) = ax2 + bx + c (a ≠ 0)
có biệt thức ∆ = b2 – 4ac.
– Nếu ∆ < 0 thì với mọi x, f(x) có cùng dấu với hệ số a.
– Nếu ∆ = 0 thì f(x) có nghiệm kép x = -b/2a, với mọi x ≠ f(x) có cùng dấu với hệ số a.
– Nếu ∆ > 0, f(x) có 2 nghiệm x1, x2 (x1 < x2) và luôn cùng dấu với hệ số a với mọi x ngoài đoạn [x1; x2] và luôn trái dấu với hệ số a với mọi x trong đoạn (x1; x2).
2. Bất phương trình bậc hai một ẩn.
Là mệnh đề chứa một biến có một trong các dạng:
ax2 + bx + c > 0, ax2 + bx + c < 0, ax2 + bx + c ≥ 0, ax2 + bx + c ≤ 0 trong đó vế trái là một tam thức bậc hai.
Để giải bất phương trình bậc hai một ẩn ta dùng định lí về dấu của tam thức bậc hai.
[su_button url=”https://www.nguyentheanh.com/dang-ki-khoa-hoc-cua-thay-nguyen-the-anh” target=”blank” style=”3d” background=”#ef9a2d” size=”5″ center=”yes” icon=”icon: arrow-down” icon_color=”#ffffff” text_shadow=”0px 0px 0px #09184e” desc=”Hoặc gọi thầy: 0986.683.218″]ĐĂNG KÍ HỌC LỚP 10[/su_button]
B. Bài tập về dấu tam thức bậc hai
Bài 1 trang 105 SGK Đại số 10
1. Xét dấu các tam thức bậc hai
a) 5x2 – 3x + 1; b) – 2x2 + 3x + 5;
c) x2 + 12x + 36; d) (2x – 3)(x + 5).
Hướng dẫn.
a) ∆ = (- 3)2 – 4.5 < 0 => 5x2 – 3x + 1 > 0 ∀x ∈ R (vì luôn cùng dấu với 5 > 0).
b) – 2x2 + 3x + 5 = 0 <=> x1 = – 1, x2 = 5/2
– 2x2 + 3x + 5 <0 với x >5/2 or x<-1
– 2x2 + 3x + 5 > 0 với – 1 < x < 5/2
c) ∆’ = 62 – 36 = 0 => x2 + 12x + 36 > 0 ∀x ≠ – 6.
d) (2x – 3)(x + 5) = 0 <=> x1 = – 5, x2 = 3/2
Hệ số của tam thức bằng 2 > 0. Do đó:
(2x – 3)(x + 5) > 0 với x >3/2 or x<-5
(2x – 3)(x + 5) < 0 với -5<x <3/2
Bài 2 trang 105 SGK Đại số 10
2. Lập bảng xét dấu các biểu thức sau
a) f(x) = (3x2 – 10x + 3)(4x – 5);
b) f(x) = (3x2 – 4x)(2x2 – x – 1);
c) f(x) = (4x2 – 1)(- 8x2 + x – 3)(2x + 9);
d) f(x) =
Hướng dẫn.
a) 3x2 – 10x + 3 = 0 <=> x1 = 1/3, x2 = 3
Bảng xét dấu:
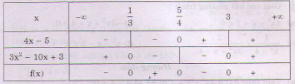
Kết luận: f(x) < 0 với x ∈ (-∞; 1/3) ∪ (3; +∞).
b) Bảng xét dấu:
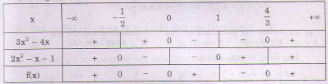
c) Ta có: – 8x2 + x – 3 < 0 ∀x (vì ∆ = 1 – 4.(- 3)(- 8) < 0, a = -8 <0).

d) Ta có: 4x2 + x – 3 = 0 <=> x1 = – 1, x1 = 3/4
Bảng xét dấu:
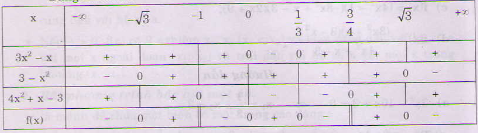
Bài 3 trang 105 SGK Đại số 10
3. Giải các bất phương trình sau
a) 4x2 – x + 1 < 0; b) – 3x2 + x + 4 ≥ 0;
c) d) x2 – x – 6 ≤ 0.
Hướng dẫn.
a) Tam thức f(x) = 4x2 – x + 1 có hệ số a = 4 > 0 biệt thức ∆ = 12 – 4.4 < 0. Do đó f(x) > 0 ∀x ∈ R.
Bất phương trình 4x2 – x + 1 < 0 vô nghiệm.
b) f(x) = – 3x2 + x + 4 = 0 <=> x1 = – 1, x2 = 4/3
– 3x2 + x + 4 ≥ 0 <=> – 1 ≤ x ≤ 4/3
c) <=>
<=>
Lập bảng xét dấu vế trái:

Tập nghiệm của bất phương trình S = (-∞; – 8) ∪ (- 2; -4/3 ∪ (1; 2).
d) Tập nghiệm S =[- 2; 3].
Bài 4 trang 105 SGK Đại số 10
4. Tìm các giá trị của tham số m để các phương trình sau vô nghiệm
a) (m – 2)x2 + 2(2m – 3)x + 5m – 6 = 0;
b) (3 – m)x2 – 2(m + 3)x + m + 2 = 0.
Hướng dẫn.
a) Với m = 2 phương trình trở thành 2x + 4 = 0 có 1 nghiệm. Loại giá trị m = 2.
Phương trình vô nghiệm nếu:
<=> m < 1 ∪ m > 3.
b) Với m = 3, phương trình trở thành: – 6x + 5 = 0 có nghiệm. Loại trường hợp m = 3.
Phương trình vô nghiệm vô khi và chỉ khi:
<=> < m < – 1.
[metaslider id=2017]