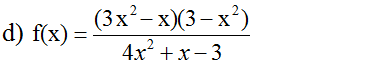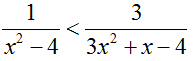DẤU CỦA TAM THỨC BẬC HAI

Xem thêm về lý thuyết tam thức bậc hai, tam thức bậc 2

Dấu của tam thức bậc 2

Định lí Viet thuận và đảo trong phương trình bậc hai -tam thức bậc hai

Các bài tập về tam thức bậc 2 lớp 8

Các bài tập về tam thức bậc 2 lớp 10

1.Khái niệm

 Tam thức bậc hai (một ẩn) là đa thức có dạng $f\left(x\right)=a{x}^2+bx+c$ trong đó  là biến $a,b,c$là các số đã cho, với $a\ne 0$.

Định lí. Cho tam thức bậc hai $f\left(x\right)=a{\mathrm{x^}}^2+bx+c(a\ne 0)$ có biệt thức    $\Delta ={\mathrm{b^}}^2–4ac$

– Nếu $\Delta <0$ thì với mọi $x,f\left(x\right)$ có cùng dấu với hệ số $a$.

– Nếu $\Delta =0$ thì $f\left(x\right)$ có nghiệm kép $x=-\frac{\mathrm{b/}}{2a}$, với mọi $x\ne -\frac{\mathrm{b/}}{2}$  có cùng dấu với hệ số .

– Nếu $\Delta >0,f\left(x\right)$ có  nghiệm $x_1,x_2(x_1<x_2)$và luôn cùng dấu với hệ số $a$ với mọi $x$ ngoài đoạn $[x_1;x_2]$ và luôn trái dấu với hệ số $a$ với mọi $x$ trong đoạn $(x_1;x_2)$

2.Các dạng bài tập

3.Các bài tập ứng dụng

1. So sánh 1 với nghiệm của phương trình 2x² – 18x + 17 = 0 [TD10BD70]
2. So sánh – 2 với nghiệm của phương trình f(x) = (m² + 1)x² – 5(m² + 1)x – m² + m – 1 = 0 [TD11BD70]
3. Tìm m để các phương trình sau có hai nghiệm
   1. mx² + (m – 1)x + 3 – 4m = 0 và thoả mãn x₁ < 2 < x₂ [VD1TTM19]
   2. (m + 1)x² – (m – 3)x + m + 1 = 0 và thoả mãn -1 < x₁ ≤ x₂
   3. (m + 1)x² + mx + 3 = 0 và thoả mãn x₁ < – 2 < 1 < x₂ [VD-TTM27]
   4. x² – 2mx + m = 0 và thoả mãn x₁, x₂ (-1;3)
   5. x² – 2x – 3m = 0 và thoả mãn
4. Tìm m sao cho
   1. f(x) = 2x² – 2(m + 1)x + 2m + 1 > 0
   2. f(x) = (m – 1)x² – (m – 1)x + 1 – 2m ≤ 0 [VD1TTM17]
5. Tìm m để bất phương trình f(x) = mx² – (2m – 1)x + m + 1 < 0 vô nghiệm. [VD2TTM17]
6. Định m để với [VD3TTM19]
7. Tìm m để phương trình sau có nghiệm
   1. (x² + 2x)² – 4m(x² + 2x) + 3m + 1 = 0 [VD1TTM23]
   2. x⁴ + mx³ + 2mx² + mx + 1 = 0 [VD!TTM31]
8. Tìm m để phương trình (m + 1)x² – 3mx + 4m = 0 có duy nhất một nghiệm lớn hơn 1. [VD3TTM25]
9. Tìm m sao cho f(x) = (m + 2)x² – 2(m + 3)x – m + 3 > 0 với [VD1TTM34]
10. CMR phương trình f(x) = m(x² – 9) + x(x – 5) = 0 luôn có nghiệm. [VD-TTM38]
11. Giải và biện luận phương trình [TD13BD71]
12. Với giá trị nào của m thì: [TD15BD74]
13. Tim m để [TD21BD77]

4.Giải bài tập SGK

Bài 1 (trang 105 SGK Đại Số 10): Xét dấu các tam thức bậc hai:

a) 5x² – 3x + 1 ;      b) -2x² + 3x + 5

c) x² + 12x + 36 ;      d) (2x – 3)(x + 5)

Lời giải

a) f(x) = 5x² – 3x + 1 có Δ = 9 – 20 = -11 < 0 và có hệ số a = 5 > 0 nên f(x) > 0 ∀x ∈ R

b) f(x) = -2x² + 3x + 5 có Δ = 9 + 40 = 49

Tam thức có hai nghiệm phân biệt x₁ = -1; x₂ = 5/2

Ta có bảng xét dấu:

Vậy f(x) > 0 ⇔ x ∈ (-1; 5/2)

f(x) = 0 ⇔ x = -1 ; x = 5/2

f(x) < 0 ⇔ x ∈ (-∞; -1) ∪ (5/2; +∞)

c) f(x) = x² + 12x + 36 có Δ = 0 nên có một nghiệm là x = -6

Ta có bảng xét dấu:

Vậy f(x) > 0 ⇔ x ≠ -6

f(x) = 0 ⇔ x = -6

(hoặc có thể phân tích f(x) = (x + 6)² ≥ 0 ∀x ∈ R)

d) f(x) = (2x – 3)(x + 5) có hai nghiệm phân biệt x₁ = 3/2; x₂ = -5

Ta có bảng xét dấu:

Vậy f(x) > 0 ⇔ x ∈ (-∞; -5) ∪ (3/2; +∞)

f(x) = 0 ⇔ x = -5 ; x = 3/2

f(x) < 0 ⇔ x ∈ (-5; 3/2)

Bài 2 (trang 105 SGK Đại Số 10): Lập bảng xét dấu các biểu thức sau:

a) f(x) = (3x² – 10x + 3)(4x – 5)

b) f(x) = (3x² – 4x)(2x² – x – 1)

c) f(x) = (4x² – 1)(-8x² + x – 3)(2x + 9)

Lời giải

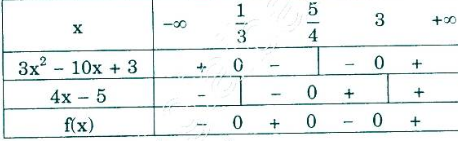
a) f(x) = (3x² – 10x + 3)(4x – 5)

Bảng xét dấu:

Vậy: f(x) > 0 ⇔ x ∈ (1/3; 5/4) ∪ x ∈ (3; +∞)

f(x) = 0 ⇔ x = 1/3; 5/4; 3

f(x) < 0 ⇔ x ∈ (-∞; 1/3) ∪ x ∈ (5/4; 3)

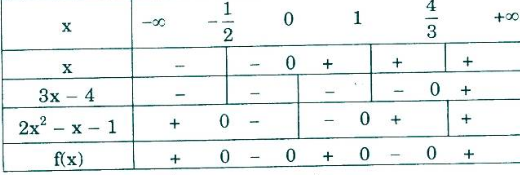
b) f(x) = (3x² – 4x)(2x² – x – 1) = x(3x – 4)(2x² – x – 1)

Bảng xét dấu:

Vậy: f(x) > 0 ⇔ x ∈ (-∞; -1/2) ∪ x ∈ (0; 1) ∪ x ∈ (4/3; +∞)

f(x) = 0 ⇔ x = -1/2; 0; 1; 4/3

f(x) < 0 ⇔ x ∈ (-1/2; 0) ∪ x ∈ (1; 4/3)

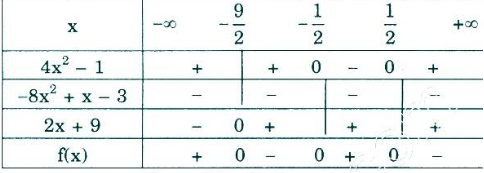
c) f(x) = (4x² – 1)(-8x² + x – 3)(2x + 9)

Bảng xét dấu:

Vậy: f(x) > 0 ⇔ x ∈ (-∞; -9/2) ∪ x ∈ (-1/2; 1/2)

f(x) = 0 ⇔ x = -9/2; -1/2; 1/2

f(x) < 0 ⇔ x ∈ (-9/2; -1/2) ∪ x ∈ (1/2; +∞)

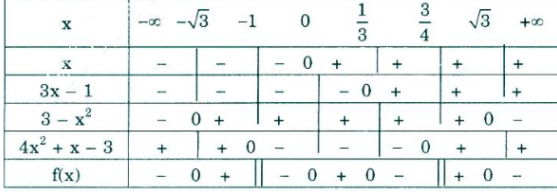
Bảng xét dấu:

Vậy: f(x) > 0 ⇔ x ∈ (-√3; -1) ∪ x ∈ (0; 1/3) ∪ x ∈ (3/4; √3)

f(x) = 0 ⇔ x = ±√3; 0; 1/3

f(x) < 0 ⇔ x ∈ (-∞; -√3) ∪ x ∈ (-1; 0) ∪ x ∈ (1/3; 3/4) ∪ x ∈ (√3; +∞)

Bài 3 (trang 105 SGK Đại Số 10): Giải các bất phương trình sau

a) 4x² – x + 1 < 0

b) -3x² + x + 4 ≥ 0

c) 

d) x² – x – 6 ≤ 0

Lời giải

a) 4x² – x + 1 < 0

Xét f(x) = 4x² – x + 1 có: Δ = 1 – 16 = -15 < 0 và a = 4 > 0 nên f(x) > 0 ∀x ∈ R

Vậy bất phương trình đã cho vô nghiệm.

(Hoặc ta có: 4x² – x + 1 = (2x)² – 2.2x.1/4 + 1/16 + 15/16 = (2x – 1/4)² + 15/16 > 0 ∀x ∈ R)

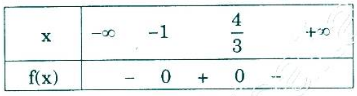
b) -3x² + x + 4 ≥ 0

Xét f(x) = -3x² + x + 4 có hai nghiệm phân biệt: x₁ = -1; x₂ = 4/3

Ta có bảng xét dấu:

Nên f(x) > 0 ⇔ x ∈ (-1; 4/3)

f(x) = 0 ⇔ x = -1; x = 4/3

Vậy tập nghiệm của bất phương trình là: T = [-1; 4/3]

c) 

Nên f(x) < 0 ⇔ x ∈ (-∞; -8) ∪ (-2; -4/3) ∪ (1; 2)

Vậy tập nghiệm của bất phương trình là: T = (-∞; -8) ∪ (-2; -4/3) ∪ (1; 2)

d) x² – x – 6 ≤ 0

Xét f(x) = x² – x – 6 có hai nghiệm phân biệt: x₁ = -2; x₂ = 3

Bảng xét dấu:

Nên f(x) < 0 ⇔ x ∈ (-2; 3) và f(x) = 0 ⇔ x = -2; x = 3

Vậy tập nghiệm của bất phương trình là: T = [-2; 3]

Bài 4 (trang 105 SGK Đại Số 10): Tìm các giá trị của tham số m để các phương trình sau vô nghiệm

a) (m – 2)x² + 2(2m – 3)x + 5m – 6 = 0

b) (3 – m)x² – 2(m + 3)x + m + 2 = 0

Lời giải

a) Đặt f(x) = (m – 2)x² + 2(2m – 3)x + 5m – 6

– Nếu m – 2 = 0 ⇔ m = 2 khi đó phương trình f(x) = 0 trở thành:

2x + 4 = 0 ⇔ x = -2 hay phương trình có một nghiệm

Do đó m = 2 không phải là giá trị cần tìm.

– Nếu m – 2 ≠ 0 ⇔ m ≠ 2 ta có:

Δ’ = (2m – 3)² – (m – 2)(5m – 6)

= 4m² – 12m + 9 – 5m² + 6m + 10m – 12

= -m² + 4m – 3 = (-m + 3)(m – 1)

Phương trình f(x) = 0 vô nghiệm khi và chỉ khi Δ’ < 0

⇔ (-m + 3)(m – 1) < 0 ⇔ m ∈ (-∞; 1) ∪ (3; +∞)

Vậy với m ∈ (-∞; 1) ∪ (3; +∞) thì phương trình vô nghiệm.

b) Đặt f(x) = (3 – m)x² – 2(m + 3)x + m + 2

– Nếu 3 – m = 0 ⇔ m = 3 khi đó phương trình f(x) = 0 trở thành:

-6x + 5 = 0 ⇔ x = 5/6 là nghiệm của phương trình.

Do đó m = 3 không phải là giá trị cần tìm.

– Nếu 3 – m ≠ 0 ⇔ m ≠ 3 ta có:

Δ’ = (m + 3)² – (3 – m)(m + 2)

= m² + 6m + 9 – 3m – 6 + m² + 2m

= 2m² + 5m + 3 = (2m + 2)(m + 3/2)

Phương trình f(x) = 0 vô nghiệm khi và chỉ khi Δ’ < 0

⇔ (2m + 2)(m + 3/2) < 0 ⇔ m ∈ (-3/2; -1)

Vậy với m ∈ (-3/2; -1) thì phương trình vô nghiệm.