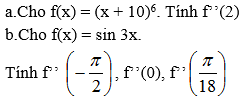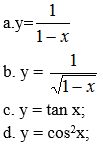Lý thuyết và bài tập đạo hàm cấp hai đạo hàm cấp cao
Lý thuyết đạo hàm cấp hai (định nghĩa đạo hàm cấp 2)

1. Định nghĩa đạo hàm cấp 2
Giả sử hàm số f(x)f(x) có đạo hàm f′(x)f′(x). Nếu f′(x)f′(x) cũng có đạo hàm thì ta gọi đạo hàm của nó là đạo hàm cấp hai của f(x)f(x) và kí hiệu f“(x)f”(x): (f′(x))′=f“(x)(f′(x))′=f”(x) .
Tương tự: (f′′(x))′=f“′(x)(f″(x))′=f”′(x) hoặc f(3)(x)f(3)(x)
…
(f(n−1)(x))′=f(n)(x)(f(n−1)(x))′=f(n)(x), n∈N∗n∈N∗, n≥4n≥4.
Ở đây kí hiệu f(0)(x)=f(x)f(0)(x)=f(x); f(n)(x)f(n)(x) là đạo hàm cấp nn của hàm số f(x)f(x).
2. Ý nghĩa cơ học của đạo hàm cấp hai
Đạo hàm cấp hai f“(t)f”(t) là gia tốc tức thời của chuyển động s=f(t)s=f(t) tại thởi điểm tt.
Bài 1 (trang 174 SGK Đại số 11):Tính đạo hàm cấp 2
Lời giải:
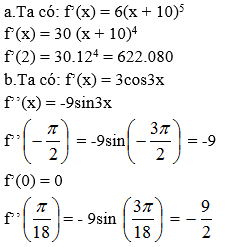
Bài 2 (trang 174 SGK Đại số 11): Tính đạo hàm cấp hai của các hàm số sau:
Lời giải Bài 2 (trang 174 SGK Đại số 11