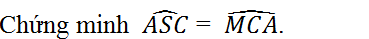Bài 5. Góc có đỉnh ở bên trong đường tròn. Góc có đỉnh ở bên ngoài đường tròn
A. Lý thuyết

1. Góc có đỉnh ở bên trong đường tròn

Số đo của góc có đỉnh ở bên trong đường tròn bằng nửa tổng số đo hai cung bị chắn.

                $\widehat{BEC}$= ($\frac{sđ{BC}^{}+sđ{A\mathrm{D)/}}^{}}{2}$

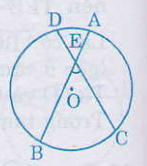
2. Góc có đỉnh ở bên ngoài đường tròn

Số đo của góc có đỉnh ở bên trong đường tròn bằng nửa hiệu số đo hai cung bị chắn.

sđ $\widehat{BEC}$=($\frac{sđ{BC}^{}-sđ{A\mathrm{D)/}}^{}}{2}$, sđ $\widehat{AEC}$ =($\frac{sđ{AmC}^{}-sđ{An\mathrm{C)/}}^{}}{2}$

B. Bài tập 

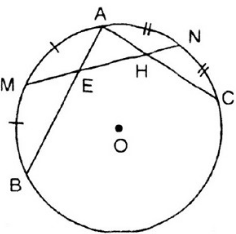
Bài 36 (trang 82 SGK Toán 9 tập 2): Cho đường tròn (O) và hai dây AB, AC. Gọi M, N lần lượt là điểm chính giữa của cung AB và cung AC. Đường thẳng MN cắt dây AB tại E và cắt dây AC tại H. Chứng minh tam giác AEH là tam giác cân.

Lời giải

Bài 37 (trang 82 SGK Toán 9 tập 2): Cho đường tròn (O) và hai dây AB, AC bằng nhau. Trên cung nhỏ AC lấy một điểm M. Gọi S là giao điểm của AM và BC.

Lời giải

Bài 38 (trang 82 SGK Toán 9 tập 2): Trên một đường tròn, lấy liên tiếp ba cung AC,CD, DB sao ch0

Lời giải

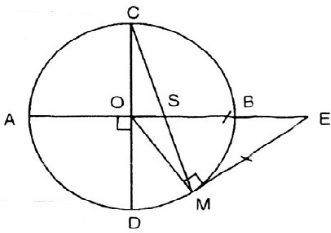
Bài 39 (trang 83 SGK Toán 9 tập 2): Cho AB và CD là hai đường kính vuông góc của đường tròn (O). Trên cung nhỏ BD lây một điểm M . Tiếp tuyến tại M cắt tia AB ở E, đoạn thẳng CM cắt AB ở S.Chứng minh ES = EM.

Lời giải

Bài 40 (trang 83 SGK Toán 9 tập 2): Qua điểm S nằm bên ngoài đường tròn (O), vẽ tiếp tuyến SA và cắt cát tuyển SBC của đường tròn . Tia phân giác của góc BAC cắt dây BC tại D. Chứng minh SA = SD.

Lời giải